腊月的季节

最小二乘法

发表于 | 分类于 | | 阅读次数

简介

我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢？监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面…

最小二乘法分析

对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：
(1)用”残差和最小”确定直线位置是一个途径。但很快发现计算”残差和”存在相互抵消的问题。
(2)用”残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以”残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。
最常用的是普通的最小二乘法:所选择的回归模型应该使所有观察值的残差平方和达到最小。即采用平方损失函数。
样本回归模型:
图片加载中...
其中ei为样本(Xi,Yi)的误差平方损失函数: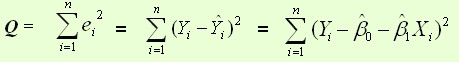
图片加载中...
则通过Q最小确定这条直线，即确定贝塔0，贝塔1，以贝塔0，贝塔1为变量，把它们看作是Q的函数，就变成了一个求极值的问题，可以通过求导数得到。求Q对两个待估参数的偏导数: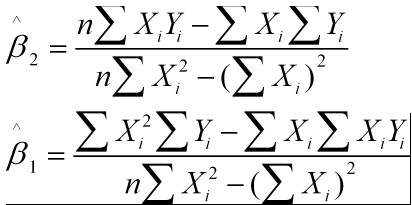
图片加载中...
根据数学知识我们知道，函数的极值点为偏导为0的点。
解得: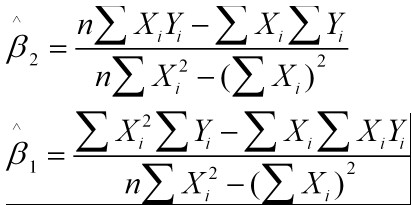
图片加载中...
这就是最小二乘法的解法，就是求得平方损失函数的极值点。

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/*
最小二乘法C++实现
参数1为输入文件
输入:x
输出:预测的y
*/
#include<iostream>
#include<fstream>
#include<vector>
using namespace std;
class LeastSquare {
    double a,b;
public:
    LeastSquare(const vector<double>& x,const vector<double>& y)
    {
    double t1=0,t2=0,t3=0,t4=0;
    for(int i=0;i<x.seze();++i){
        t1+=x[i]*x[i];
        t2+=x[i];
        t3+=x[i]*y[i];
        t4+=y[i];
}
    a=(t3*x.size()-t2*t4)/(t1*x.size()-t2*t2);//求得贝塔1
    b=(t1*t4-t2*t3)/(t1*x.size()-t2*t2);//求得贝塔2
}
    double getY(const double x) const
    {
        return a*x+b;
}
    void print() const
    {
        cout<<"y="<<a<<"x+"<<b<<"\n";
}
    int main(int argc,char *argv[])
{
    if(argc!=2)
{
    cout<<"Usage:DataFile.txt"<<endl;
    return -1;
}
    else
    {
        vector<double> x;
        ifstream in (argv[1]);
        for(double d;in>>d;)
            x.push_back(d);
        int sz = x.size();
        vector<double> y(x.begin()+sz/2,x.end());
        x.resize(sz/2);
        LeastSquare(x,y);
        ls.print();
        cout<<"Input x:\n";
        double x0;
        while(cin>>x0)
        {
            cout<<"y="<<ls.getY(x0)<<endl;
            cout<<"Input x:\n";
        }
    }
}
}

最小二乘法与梯度下降法

最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值，那它们有什么区别呢。
相同
1.本质相同：两种方法都是在给定已知数据（independent & dependent variables）的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。
　2.目标相同：都是在已知数据的框架内，使得估算值与实际值的总平方差尽量更小（事实上未必一定要使用平方），估算值与实际值的总平方差的公式为：
图片加载中...
其中\bar{x_{i} } 为第i组数据的independent variable，y_{i} 为第i组数据的dependent variable，\beta 为系数向量。

不同
　　1.实现方法和结果不同：最小二乘法是直接对\Delta求导找出全局最小，是非迭代法。而梯度下降法是一种迭代法，先给定一个\beta ，然后向\Delta下降最快的方向调整\beta ，在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢，并且对初始点的选择极为敏感，其改进大多是在这两方面下功夫。

热评文章