腊月的季节

线性回归-最小二乘法

发表于 | 分类于 | | 阅读次数

介绍

最小二乘法的核心就是保证所有数据偏差的平方和最小。(“平方”在古时候的称谓为”二乘”)假设我们收集到一些战舰的长度和宽度数据。

1 2 3 4 5 6 7 8 9 10
长度(m) 208 152 113 227 137 238 178 104 191 130
宽度(m) 21.6 15.5 10.4 31.0 13.0 32.4 19.0 10.4 19.0 11.8

根据这些数据我们用python画出散点图
首先准备模拟数据包，我选择txt文件

1
2
3
4
5
6
7
8
9
10
208	21.6
152	15.5
113	10.4
227	31
137	13
238	32.4
178	19
104	10.4
191	19
130	11.8

书写Python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#-*- coding: utf-8 -*-
import numpy as np
import os
import  matplotlib.pyplot as plt
def drawScatterDiagram(fileName):
    xcord=[];
    ycord=[];
    fr=open(fileName)
    for line in fr.readlines():
        lineArr=line.strip().split();
        xcord.append(float(lineArr[0]));
        ycord.append(float(lineArr[1]));
    plt.scatter(xcord,ycord,c='red',marker='s')
    plt.show()
drawScatterDiagram("h:/python/algorithm/ECF/data.txt");

得到以下分析图像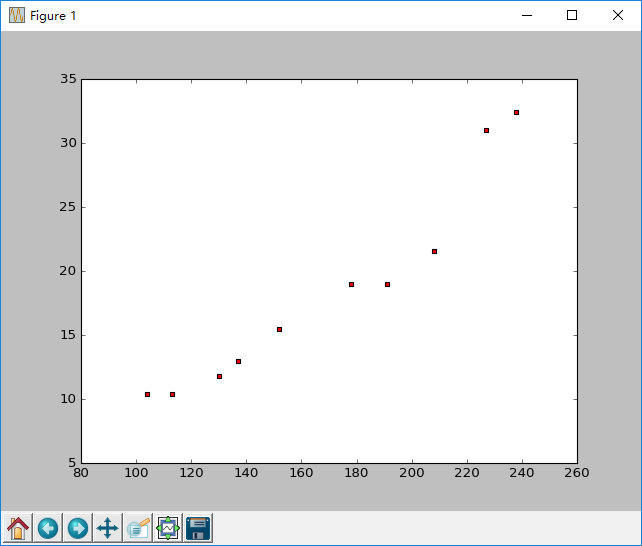
图片加载中
假如我们取前两个点(238,32.4) (152,15.5)就可以得到两个方程
152a+b=15.5
238a+b=32.4
解得a=0.1965116 b=-14.36976
这样我们就可以得到一个拟合图:
新的问题是，这样的a,b是不是最优解，用专业的说法就是a,b是不是模型的最优化参数?在回答这个问题之前，我们先解决另外一个问题，a,b满足什么条件才是最好的?答案是:保证所有数据偏差的平方和最小。至于原理，我们会在后面讲，先来看看怎么利用这个工具来计算最好的a和b。
假设所有数据的平方和为M:则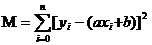图片加载中
我们现在要做的就是求使得M最小的a和b。请注意这个方程中,我们已知yi和xi，那其实这个方程就是一个以(a,b)为自变量，M为因变量的二元函数。
回想一下高数中怎么对一元函数求极值。我们用的是导数这个工具。那么在二元函数中，我们依然用导数 。只不过这里的导数有了新的名字”偏导数”。偏导数就是把两个变量中的一个视为常数来求导。通过对M来求偏导数，我们得到一个方程组
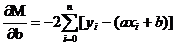
图片加载中
图片加载中
这两个方程中xi和yi都是知道的
很容易就求得a和b了。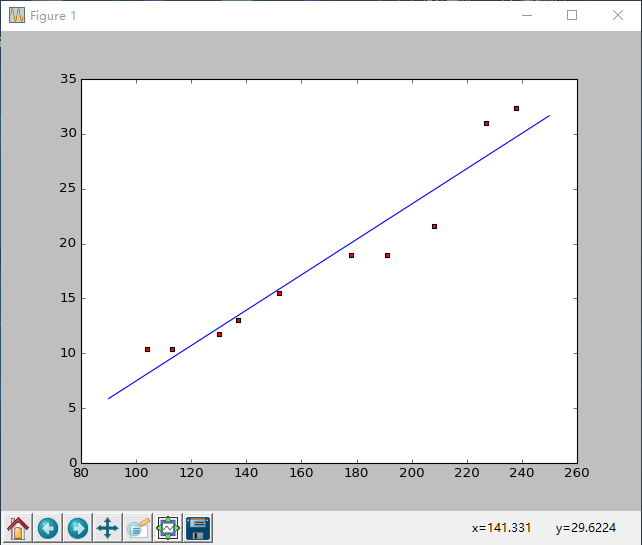
图片加载中
python代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#-*- coding: utf-8 -*-
import numpy as np
import os
import  matplotlib.pyplot as plt
def drawScatterDiagram(fileName):
    xcord=[];
    ycord=[];
    fr=open(fileName)
    for line in fr.readlines():
        lineArr=line.strip().split();
        xcord.append(float(lineArr[0]));
        ycord.append(float(lineArr[1]));
    plt.scatter(xcord,ycord,c='red',marker='s')
    a=0.1612;b=-8.6394
    x=np.arange(90.0,250.0,0.1)
    y=a*x+b
    plt.plot(x,y)
    plt.show()
drawScatterDiagram("h:/python/algorithm/ECF/data.txt");

原理探究

数据拟合中，为什么要让模型的预测数据与实际数据之差的平方而不是绝对值和最小来优化模型参数？

热评文章